Làm thế nào để giải quyết các bài toán gặp phải khi lập trình? 🤔

Summary
HideGiải quyết các bài toán là việc mà chúng ta đều gặp phải hằng ngày trong mọi việc mà chúng ta làm. Lập trình cũng không phải là ngoại lệ. Hẳn là nhiều người khi mới học lập trình đều đã từng cảm thấy mông lung không biết phải giải quyết một bài toán như thế nào. Bài viết này sẽ chia sẻ hướng và các bước đơn giản để giải quyết một bài toán.
1. Đọc và hiểu yêu cầu. 🔎
Đọc kỹ và phân tích yêu cầu có lẽ là công việc quan trọng nhất khi bạn phải giải quyết một bài toán. Đọc kỹ yêu cầu của bài toán giúp bạn xác định hướng giải quyết bài toán đó, không bị lạc đề hay bỏ lỡ những thông tin quan trọng.
1.1. Xác định đầu vào, đầu ra của bài toán. ⌨
Thường, trong đề của các bài toán sẽ có đầu vào (Input) và đầu ra (Output). Đây là thông tin quan trọng mà bạn cần lưu ý. Đầu ra của bài toán chính là một gợi ý về cách bắt đầu của bài toán. Còn đầu ra thì đương nhiên là quan trọng rồi. Như mẹ nhờ bạn đi mua táo, bạn lại mua cam về là thể nào cũng ăn đòn.
Để tìm được đầu vào của bài toán, hãy tập trung vào những danh từ trong đề bài, để ý xem đề bài có những thông tin gì.
VD:
Tính diện tích hình chữ nhật với chiều dài 10cm và chiều rộng 2cm.
Input: chiều dài và chiều rộng của hình chữ nhật.
!!!LƯU Ý: không phải tất cả bài toán đều cho bạn đầu vào cụ thể mà chúng sẽ được cho khi chạy code. Bài toán trên có thể hỏi rằng “tính diện tích hình chữ nhật với chiều dài và chiều rộng được nhập” thay vì cho sẵn 10cm và 2cm.
Tạo function return index của element x trong array A.
Input: element x và array A.
Khi đã xác định được đầu vào của bài toán, việc tiếp theo bạn cần làm là tìm đầu ra của bài toán. Một số từ gợi ý cho ta về đầu ra của bài toán là các động từ như: tìm, tính, find, calculate, return, …
VD:
Tính diện tích hình chữ nhật với chiều dài 10cm và chiều rộng 2cm.
Output: diện tích của hình chữ nhật đã cho.
Tạo function return index của element x trong array A.
Output: index của element x.
1.2. Xác định yêu cầu xử lý của bài toán. 🖥
Một số bài toán chỉ cho Input và Output của bài toán; bạn phải tự tìm cách để xử lý Input thành Output. Một số khác sẽ có các bước, công việc cụ thể mà bạn phải làm theo.
VD:
Tính GPA của 3 môn học A, B, C.
Processing: GPA = (A + B + C) / 3.
Write an algorithm that asks the user for a positive number. If the input is not a positive number, the program should keep asking until the user enters a positive number. Keeps track of how many time the user enters a “wrong” number and print out at the end.
Viết thuật toán hỏi người dùng nhập một số dương. Nếu input không phải là một số dương tiếp tục hỏi cho đến khi nhận được số dương. Lưu lại số lần người dùng nhập một số “sai” và in ra khi kết thúc.
Processing:
- Hỏi người dùng một số.
- Kiểm tra số đó có dương không.
- Nếu không, hỏi lại và tăng số lần nhập sai lên một.
- Nếu đúng, dừng lại và in ra số lần nhạp sai..
2. Chia nhỏ bài toán. ➗
2.1. Divide and Conquer (chia để trị). 🎮
Nếu gặp một bài toán đơn giản thì bạn có thể nghĩ ra được đáp án luôn. Tuy nhiên khi phải đối mặt với các bài toán phức tạp thì bạn khó có thể nghĩ ra được hướng giải quyết luôn. Vì vậy mà bạn nên chia nhỏ bài toán đó thành các phần dễ làm hơn.
VD:
Bay từ Hà Nội vào Sài Gòn.
Các việc nhỏ:
- Đặt vé máy bay.
- Đi đến sân bay.
- Quay story.
- Lên máy bay.
- Ngủ.
Tạo một trang Web
Các việc nhỏ:
- Tạo header.
- Thêm nội dung, hình ảnh, video.
- Chỉnh sửa css để trang web đẹp hơn.
- …
2.2. Giải quyết các bài toán nhỏ hơn. 💡
Từ những phần nhỏ này ta lại có thể chia thành những công việc cụ thể hơn:
- Quay story: tìm góc đẹp, chọn filter, diễn sâu,…
- Tạo header: thêm tên, logo, navigation (điều hướng),…
Ngoài ra, các bài toán có thể khác nhau nhưng chúng hầu hết đều được xây dựng từ những phần, công việc giống nhau. Nhận diện (Pattern Recognition) được dạng của các công việc nhỏ này rất hữu ích bởi vì có thể bạn đã từng giải, từng viết code cho công việc đó từ trước.
Bắt đầu từ Input, Output, kết hợp với các bước nhỏ, từ đó bạn có thể xây dựng được cách giải quyết cho bài toán.
3. Giải tay. ✏
Code đơn giản chỉ là ngôn ngữ hay công cụ mà chúng ta dùng để giải quyết vấn đề. Như Tiếng Anh, Tiếng Pháp, Tiếng Việt,… chỉ là một công cụ để bạn bày tỏ suy nghĩ của mình thành lời, thành văn. Khi phải giải một bài toán hãy bắt đầu từ giải nó bằng tay trước. Hãy nghĩ nếu với đề bài đã cho, thường bạn giải quyết nó như thể nào. Từ đó, bạn có thể ghi lại các bước mà bạn phải làm để giải bài toán đó.
VD:
Tìm max, min của trong các số a, b, c, d, e
Giả dụ bạn được cho các số 5, 12, -2 , 2, 4.
- Ta sẽ nhìn số thứ nhất (5) và so sánh với số thứ hai (12):
12 > 5 nên ta nhớ 12 đang là lớn nhất.
- Tiếp tục so sánh 12 với số thứ ba (-2):
12 > -2 nên ta vẫn giữ 12 là số lớn nhất.
- Tiếp tục so sánh 12 với số thứ tư (2):
12 > 2 nên ta vẫn giữ 12 là số lớn nhất.
- Tiếp tục so sánh 12 với số thứ năm (4):
12 > 4 nên ta vẫn giữ 12 là số lớn nhất.
⇒ Vậy số lớn nhất là 12.
Ta có thể viết lại những bước đó thành:
Các số được cho ta có thể lưu vào một array (một danh sách) để dễ truy cập.
Đầu tiên lấy số đầu là số đang lớn nhất.
Và vị trí của số đó trong array là 0.
Lặp lại cho đến hết array (đến hết các số):
- Nếu số đang kiểm tra lớn hơn số đang lớn nhất; đổi số đang lớn nhất thành số đó, và vị trí số lớn nhất thành vị trí hiện tại.
- Nếu không thì tiếp tục kiểm tra số tiếp theo.
1
2
3
4
5
6
7
8
9
10
11
array ← [a, b, c, d, e]
max_element ← array[0]
max_index ← 0
for i ← 0 to length(array) - 1:
element = array[i]
if element > max_element:
max_element ← element
max_index ← i
print max_element, max_index
Để tìm số nhỏ nhất ta cũng làm gần tương tự như trên:
- Ta sẽ nhìn số thứ nhất (5) và so sánh với số thứ hai (12):
5 < 12 nên ta nhớ 5 đang là nhỏ nhất.
- Tiếp tục so sánh 5 với số thứ ba (-2):
-2 < 5 nên ta chuyển -2 là số nhỏ nhất.
- Tiếp tục so sánh -2 với số thứ tư (2):
-2 < 2 nên ta vẫn giữ -2 là số nhỏ nhất.
- Tiếp tục so sánh -2 với số thứ năm (4):
-2 < 4 nên ta vẫn giữ -2 là số nhỏ nhất.
⇒ Vậy số nhỏ nhất là -2.
Ta có thể viết lại những bước này thành:
Các số được cho ta có thể lưu vào một array (một danh sách) để dễ truy cập.
Đầu tiên lấy số đầu là số đang nhỏ nhất.
Và vị trí của số đó trong array là 0.
Lặp lại cho đến hết array (đến hết các số):
- Nếu số đang kiểm tra nhỏ hơn số đang nhỏ nhất; đổi số đang nhỏ nhất thành số đó, và vị trí số nhỏ nhất thành vị trí hiện tại.
- Nếu không thì tiếp tục kiểm tra số tiếp theo.
1
2
3
4
5
6
7
8
9
10
11
array ← [a, b, c, d, e]
min_element ← array[0]
min_index ← 0
for i ← 0 to length(array) - 1:
element = array[i]
if element < min_element:
min_element ← element
min_index ← i
print min_element, min_index
4. Test và tối ưu hóa thuật toán. 🧪
Test thử thuật toán tìm ra các lỗi sai và giúp cải thiện hiệu năng của thuật toán. Từ đó bạn không phải tốn thời gian viết code và chỉnh sửa code nhiều lần.
Chúng ta hãy thử chạy thuật toán tìm số lớn nhất và nhỏ nhất ở trên. Chúng ta sẽ chạy từng bước một và ghi lại vào bảng để xem thuật toán chạy như thế nào, có đúng không.
Cho [a, b, c, d, e] = [2, 3, 1, 10, -3]
| i | element | element > max_element | max_element | max_index |
|---|---|---|---|---|
| 0 | 2 | 2 | 0 | |
| 1 | 3 | True | 3 | 1 |
| 2 | 1 | False | 3 | 1 |
| 3 | 10 | True | 10 | 3 |
| 4 | -3 | False | 10 | 3 |
Thuật toán đã chạy đúng, số lớn nhất là số thứ 10 và vị trí 3 trong arrray (số thứ tư)
| i | element | element < min_element | min_element | min_index |
|---|---|---|---|---|
| 0 | 2 | 2 | 0 | |
| 1 | 3 | False | 2 | 0 |
| 2 | 1 | True | 1 | 2 |
| 3 | 10 | False | 1 | 2 |
| 4 | -3 | True | -3 | 4 |
Thuật toán đã chạy đúng, số nhỏ nhất là số thứ -3 và vị trí 4 trong arrray (số thứ năm)
5. Viết và chạy code. 🤖
Trong lập trình, viết code có khi lại là phần đơn giản nhất khi giải một bài toán. Bởi vì ở bước này, bạn chỉ cần dịch lại thuật toán đã viết thành code. Chạy code cũng là một phần rất quan trọng. Bước này sẽ kiểm tra xem code đã đúng với thuật toán hay chưa, code chạy có hiệu quả hay không, phải chỉnh sửa chỗ nào.
Thuật toán tìm số lớn nhất và nhỏ nhất ở trên viết bằng Python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def find_max(array):
max_element = array[0]
max_index = 0
for index, element in enumerate(array):
if element > max_element:
max_element = element
max_index = index
return max_element, index
def find_min(array):
min_element = array[0]
min_index = 0
for index, element in enumerate(array):
if element < min_element:
min_element = element
min_index = index
return min_element, index
Ví dụ. 💪
Chúng ta đã đi qua hết các bước cơ bản để giải một bài toán, bây giờ hãy cùng kết hợp chúng lại nhé. Chúng ta sẽ thử giải bài toán:
Nhập một số x, trả về 1 nếu x là số nguyên tố, nếu không trả về 0.
Bước 1: phân tích yêu cầu:
- Input: 1 số x
- Output: 1 nếu x là số nguyên tố nếu không trả về về 0.
Bước 2: chia nhỏ bài toán:
Chúng ta có thể nhìn ra một số công việc phải làm:
- Nhận vào một số x
- Kiểm tra số x có phải là số nguyên tố hay không
- Kiểm tra x có chia hết cho số nào khác 1 và chính nó không
- Nếu có trả về 1, Nếu không trả về 0
Chúng ta phải kiểm tra x có chia hết cho số từ 1 → x nên ta phải dùng vòng lặp ở đây,.
Bước 3: giải tay:
Bây giờ chúng ta hãy thử giải tay.
Ví dụ x = 7:
7 chia hết cho 1.
7 không chia hết cho 2.
7 không chia hết cho 3.
7 không chia hết cho 4.
7 không chia hết cho 5.
7 không chia hết cho 6.
7 chia hết cho 7.
⇒ 7 là số nguyên tố
Ví dụ x = 25:
25 chia hết cho 1
25 không chia hết cho 2
25 không chia hết cho 3
25 không chia hết cho 4
25 chia hết cho 5
⇒ 25 không phải là số nguyên tố
Một số trường hợp đặc biệt: 0, 1 không là số nguyên tố; 2 là số nguyên tố.
Các số nguyên tố cũng phải là số tự nhiên (>0).
Ta có thể tổng hợp một số bước để giải bài toán này:
1
2
3
4
5
6
7
8
9
is_prime(x):
if x < 2:
return 0
if x = 2:
return 1
for i ← 2 to x - 1:
if x mod i = 0:
return 0
return 1
Bước 4: test thử thuật toán:
x = 25
| i | x mod i | x mod i = 0 | Output |
|---|---|---|---|
| 2 | 1 | False | |
| 3 | 1 | False | |
| 4 | 1 | False | |
| 5 | 0 | True | |
| 0 | |||
x = 2
| x = 2 | Output |
|---|---|
| True | 1 |
x = 7
| i | x mod i | x mod i = 0 | Output |
|---|---|---|---|
| 2 | 1 | False | |
| 3 | 1 | False | |
| 4 | 3 | False | |
| 5 | 2 | False | |
| 6 | 1 | False | |
| 1 |
Ở đây chúng ta có thể nhìn thấy ta phải kiểm tra x 5 lần để xem x có chia hết cho số nào không. Ta có thể tối ưu hóa thuật toán này nếu ta chỉ kiểm tra đến sqrt(x).
Ví dụ như số 100:
100 = 2 x 50 = 4 x 25 = 5 x 20 = 10 x 10 = 20 x 5 = 25 x 4 = 50 x 2
Nếu mà 100 chia hết cho 50 thì nó phải chia hết cho 2 nếu 100 chia hết cho 25 thì phải chia hết cho 4, …
Nếu số x không chia hết cho số nào từ 2 → sqrt(x) thì nó cũng không thể chia hết cho số nào từ sqrt(x) → x.
Chính vì vậy mà ta chỉ cần kiểm tra đến sqrt(x). Ta chỉnh lại thuật toán thành:
1
2
3
4
5
6
7
8
9
is_prime(x):
if x < 2:
return 0
if x = 2:
return 1
for i ← 2 to sqrt(x):
if x mod i = 0:
return 0
return 1
Đây cũng chưa phải là thuật toán tối ưu nhất. Nếu bạn muốn tìm hiểu sâu hơn hay đọc:
Bước 5: viết và chạy code:
Thuật toán viết bằng Python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from math import sqrt
def is_prime(x):
if x < 2:
return 0
if x == 2:
return 1
i = 2
stop_place = sqrt(x)
while i <= stop_place:
if x % i == 0:
return 0
i += 1
return 1
Chúng ta có thể viết một đoạn code nhanh để test thuật toán trên:
1
2
3
4
5
while True:
x = input()
if not x.isnumeric():
break
print(is_prime(int(x)))
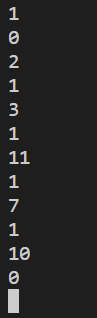
Sau một số lần thử thì ta có thể thấy thuật toán và code của chúng ta đã chạy được. Vậy là chúng ta đã hoàn thành việc giải bài toán rồi.
Tổng kết. 🎉
Kết lại, đừng nản chí khi bạn gặp công việc khó hay không biết phải giải một bài toán từ đâu. Hãy bình tĩnh, làm từng bước một. Và đột nhiên bạn sẽ nhận thấy bài toán đó dễ hơn trước. Mọi bài toán đều có thể giải được, chúng ta chỉ cần có một hướng đi đúng và sự sự kiên trì.