Sử dụng Python để mô phỏng bài toán xác suất Monty Hall
Bài toán xác suất kinh điển Monty Hall một thời đã thách thức hàng ngàn bộ não trên thế giới, từ học sinh cấp 3 cho đến những giáo sư và các chuyên gia phân tích. Tính đến ngày nay, đã có rất nhiều lời giải thích và đáp án cho câu đố này dưới góc độ toán học xuất hiện trên Internet, chủ yếu sử dụng kiến thức về xác suất thống kê. Hôm nay, UCC sẽ giới thiệu cho các bạn một hướng tiếp cận khác, đó là sử dụng ngôn ngữ lập trình Python để mô phỏng lại tình huống bài toán, từ đó đưa ra lời giải thuyết phục nhất từ số liệu đã thu được.
Nguồn gốc
Marilyn vos Savant là một phụ nữ được sách kỷ lục Guinness công nhận là người có chỉ số IQ cao nhất thế giới (228) trong khoảng thời gian từ năm 1985 đến 1989. Bà cũng là tác giả cho tạp chí Parade của Mỹ và phụ trách chuyên mục “Ask Marilyn”, nơi người đọc có thể gửi các câu đố và Vos Savant sẽ trả lời chúng.

Vào năm 1990, một độc giả tên là Craig F. Whitaker đã gửi cho tạp chí một câu đố có nội dung như sau:
Giả sử bạn đang tham gia gameshow và phải lựa chọn một trong ba cánh cửa: đằng sau một cánh cửa là một chiếc xe hơi mới tinh, còn đằng sau hai cánh cửa còn lại là hai con dê. Nếu bạn chọn đúng cánh cửa có chiếc xe, bạn sẽ được sở hữu luôn chiếc xe đó, còn nếu bạn chọn phải cánh cửa mà đằng sau nó là một con dê thì bạn phải mang con dê đó về nhà. Bạn đã chọn cánh cửa số 1, sau đó người dẫn chương trình (đã biết cánh cửa nào có dê và xe) mở một cánh cửa mà đằng sau nó là một con dê, sau đó anh ta hỏi bạn có muốn đổi lựa chọn sang cánh cửa còn lại không. Bạn có nên đổi hay không?
Marilyn đã nói rằng chúng ta nên đổi, và câu trả lời này đã thu hút rất nhiều phản hồi không đồng tình từ các độc giả, trong đó có rất nhiều tiến sĩ giáo sư từ các trường đại học. Bài toán này đã được đặt tên là “Monty Hall” vì nó rất giống với gameshow mang tên “Let’s Make a Deal” do Monty Hall làm người dẫn chương trình vào năm 1963.

Bài toán này thật ra đã được Steve Selvin giới thiệu và giải qua một lá thư gửi tạp chí khoa học American Statistician vào năm 1975, tuy nhiên nó chỉ thật sự được nhiều người biết đến nhờ danh tiếng của Marilyn vos Savant cùng với câu trả lời gây tranh cãi của bà.
Đáp án cho Bài toán
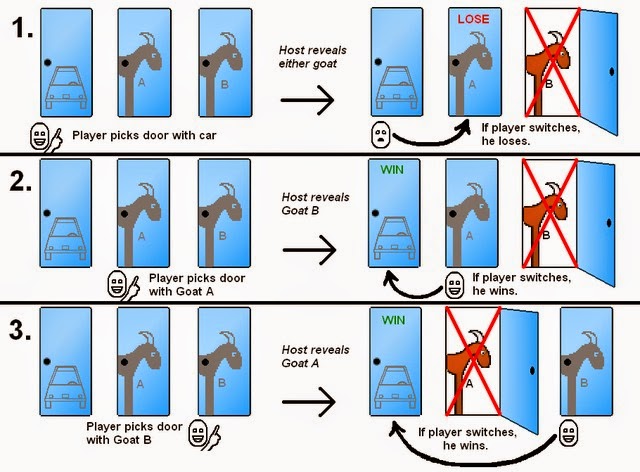
Gần như hầu hết mọi người sau khi đọc bài toán đều cho rằng sau khi người dẫn chương trình loại bỏ một cánh cửa có con dê, tỉ lệ người chơi chọn trúng cánh cửa có chiếc xe là 50%, vậy nên việc đổi cửa hay không không quan trọng. Đó là câu trả lời chính xác nếu cánh cửa mà người dẫn chương trình chọn để mở hoàn toàn ngẫu nhiên. Tuy nhiên cánh cửa mà người dẫn chương trình mở thực chất phụ thuộc vào cánh cửa người chơi chọn, do đó tỷ lệ không còn là 50/50 nữa. Bảng dưới đây sẽ miêu tả rõ nhất tỉ lệ chọn trúng chiếc xe bằng cách liệt kê tất cả các trường hợp có thể xảy ra (người chơi ban đầu chọn cánh cửa số 1):
| Cánh cửa số 1 | Cánh của số 2 | Cánh cửa số 3 | Kết quả nếu không đổi cửa | Kết quả nếu đổi cửa |
|---|---|---|---|---|
| Dê | Dê | Xe | Cầm Dê về | Cầm Xe về |
| Dê | Xe | Dê | Cầm Dê về | Cầm Xe về |
| Xe | Dê | Dê | Cầm Xe về | Cầm Dê về |
Rõ ràng, lựa chọn đổi cửa cho chúng ta 2/3 cơ hội thắng được chiếc xe. Để tìm hiểu lời giải thích toán học chi tiết cho bài toán này, Youtube có rất nhiều video. Còn nếu bạn vẫn còn hoài nghi về kết quả trên, UCC sẽ mô phỏng sẽ sử dụng Python để mô phỏng người chơi, chọn ngẫu nhiên một cánh cửa và so sánh tỉ lệ thắng giữa hai quyết định đổi cửa và không đổi cửa qua một số lượng lượt chơi lớn.
Lý do mô phỏng bài toán bằng Python
Monty Hall là một bài toán dễ gây nhầm lẫn. Ngay cả khi đã cố gắng để giải bài toán nhiều lần hay xem video giải thích toán học, logic nhiều lần thì nhiều người vẫn không tin được tỉ lệ thắng khi đổi cánh cửa là 66%. UCC cũng biết vậy, chính vì thế chúng mình đã phải tự thân xác minh thật chắc chắn xem điều đó có đúng không. Bằng cách mô phỏng lại bài toán, chúng mình đã khám phá ra được nhiều điểm hay và cuối cùng cũng hiểu được cách hoạt động của nó.
Quá trình thực hiện
Để mô phỏng trò chơi này, chúng ta cần thực hiện những bước chính sau:
- Xác định một cửa đúng.
- Người chơi chọn một cửa.
- MC mở ra một cửa sai.
- Người chơi có quyền chọn lại cửa hoặc giữ nguyên lựa chọn ban đầu.
- Kiểm tra người chơi có chọn đúng cửa hay không.
Đầu tiên chúng ta sẽ sử dụng thư viện random:
1
2
# Import thư viện random.
import random
Tiếp theo tạo một function để mô phỏng việc chọn một cánh cửa ngẫu nhiên. Ở đây, chúng ta sử dụng hàm random.randint(max, min) để lấy ngẫu nhiên một số nguyên từ 1 đến 3 đại diện cho ba cánh cửa:
1
2
3
# Chọn một cửa ngẫu nhiên số từ 1 -> 3.
def choose():
return random.randint(1, 3)
Tạo một function để chọn ra một cách cửa ngẫu nhiên khác với các cánh cửa đã được chọn. Function này sẽ giúp ta mô phỏng việc MC mở ra một cánh cửa sai và không phải cửa người chơi đã chọn:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Chọn một cửa ngẫu nhiên trong những cửa chưa được chọn.
def get_unchoosen_door(chosen_doors):
doors_selection = [1, 2, 3]
# Loại bỏ những cửa đã chọn.
for choice in chosen_doors:
if choice in doors_selection:
doors_selection.remove(choice)
# Nếu có một cửa chưa được chọn thì chọn cửa đó. Nếu không chọn ngẫu nhiên 1 trong 2 cửa còn lại.
if len(doors_selection) == 1:
return doors_selection[0]
else:
return doors_selection[random.randint(0, 1)]
Tiếp theo chúng ta sẽ tạo list RESULTS để lưu kết quả của các lần thử. Variable WINS để lưu số lượt thắng. Variable STRATEGY để lưu chiến thuật mà người chơi chọn:
1
2
3
4
5
6
7
8
9
# List để lưu lại các kết quả
RESULTS = []
# Variable lưu lại số lượt thắng
WINS = 0
# Strategy (chiến thuật) 0: giữ nguyên lựa chọn ban đầu.
# strategy (chiến thuật) 1: đổi cửa.
STRATEGY = 1
Bây giờ chúng ta sẽ vào phần chính và mô phỏng trò chơi. Đầu tiên tạo một variable để lưu số lượt thử. Các bạn có thể tùy chỉnh số lượt thử theo mong muốn của mình:
1
2
# Số lượt thử
TEST_SAMPLE = 100000
Chúng ta sẽ lặp lại trò chơi (TEST_SAMPLE) lần bằng vòng for loop và lưu lại kết quả của mỗi lượt. Trong mỗi lượt chơi, chúng ta sẽ thực hiện 5 bước đã đề cập ở trên:
1
for test in range(TEST_SAMPLE):
Variable result ở đây dùng để lưu lại kết quả của mỗi mỗi lượt chơi:
1
2
# Variable lưu lại kết quả của mỗi lượt.
result = ""
Bước 1: chọn ra một cửa đúng, việc này giống như chúng ta đang xáo trộn vị trí của các cánh cửa. Ở đây chúng ta sẽ dùng hàm choose() được tạo ở trên để mô phỏng việc đó:
1
2
# Chọn ngẫu nhiên một cửa đúng.
correct_door = choose()
Bước 2: người chơi chọn một cánh cửa ngẫu nhiên. Chúng ta lại dùng hàm choose():
1
2
# Người chơi chọn một cửa.
first_choice = choose()
Bước 3: MC sẽ mở ra một cửa sai. LƯU Ý: MC sẽ luôn mở ra cửa sai và khác với lựa chọn của người chơi. Vì vậy chúng ta dùng hàm get_unchoosen_door() đã tạo và thêm vào argument là một list gồm lựa chọn đầu tiên của người chơi và cánh cửa đúng [first_choice, correct_door]. Hàm get_unchoosen_door() sẽ loại bỏ những lựa chọn trong list đó và trả lại cánh cửa còn lại:
1
2
3
# MC mở một ra một cửa sai.
# Lưu ý: mc luôn mở ra cửa sai và không phải là cửa người chơi đã chọn.
incorrect_door = get_unchoosen_door([first_choice, correct_door])
Chúng ta thêm lựa chọn của người chơi, MC, cửa đúng vào variable result để lưu lại. Ở đây có dùng một tính năng rất hay trong python đó là template string để chèn các dữ liệu vào giữa một string mà không cần cộng các string lại. Để sử dụng template string, ta thêm chữ “f” đằng trước một string bình thường; các biến được chèn thêm sẽ được đặt trong {}:
1
2
# Lưu lại lựa chọn.
result += f"1st choice: {first_choice} | incorrect door: {incorrect_door} | correct door: {correct_door}"
Bước 4: Người chơi có quyền chọn lại cửa hoặc giữ nguyên lựa chọn ban đầu. Nếu dùng chiến thuật đổi cửa, chúng ta lại sử dụng hàm get_unchoosen_door() để chọn một cánh cửa khác với lựa chọn ban đầu và cánh cửa sai do MC mở ([first_choice, incorrect_door]). Nếu không, người chơi sẽ giữ nguyên cửa ban đầu. Ta lưu lựa chọn này lại vào variable result:
1
2
3
4
5
6
7
8
if STRATEGY:
# Nếu chọn chiến thuật 1 người chơi sẽ đổi cửa.
final_choice = get_unchoosen_door([first_choice, incorrect_door])
result += f" | final choice: {final_choice}"
else:
# Nếu chọn chiến thuật 0 người chơi sẽ giữ nguyên lựa chọn ban đầu.
final_choice = first_choice
result += " | final choice: unchanged"
Bước 5: Kiểm tra người chơi có chọn đúng cửa hay không và lưu lại kết quả:
1
2
3
4
5
6
if final_choice == correct_door:
# Nếu người chơi chọn đúng cửa, tăng số lượt thắng lên 1
WINS += 1
result += " | result: win"
else:
result += " | result: lose"
Thêm kết quả của lượt chơi này vào list các kết quả:
1
2
# Thêm kết quả của lượt chơi vào list các kết quả
RESULTS.append(result)
Vậy là chúng ta đã hoàn thành việc mô phỏng trò chơi, tiếp theo chúng ta sẽ in ra kết quả nhận được.
Tạo một vòng for loop với số loop tùy ý các bạn để in ra các kết quả:
1
2
3
# In ra một số kết quả mẫu
for r in range(5):
print(RESULTS[r])
Chúng ta cũng có thể in ra thêm một số thông tin tổng hợp. Ở đây cũng có một tính năng hữu ích của Python đó là inline if else. Cấu trúc inline if else như sau:
*(kết quả nếu điều kiện đúng)* if *(điều kiện)* else *(kết quả nếu điều kiện sai)*
Tính năng này rất hữu ích trong các trường hợp bạn cần trả lại một kết quả nhanh với điều kiện đơn giản:
1
2
3
4
5
# In ra tổng kết.
print(f"Test sample: {TEST_SAMPLE}")
print(f"Strategy: {STRATEGY} ({'change door when offered' if STRATEGY else 'do not change door when offered'})")
print(f"Wins: {WINS}")
print(f"Winning probability: {WINS / TEST_SAMPLE}")
Bây giờ chỉ còn bước chạy thôi :))
Các bạn nhớ chỉnh variable STRATEGY (chiến thuật) để xem kết quả nhé:
Đúng theo dự đoán, nếu người chơi giữ nguyên lựa chọn ban đầu của mình và không thay đổi cửa thì tỷ lệ thắng sẽ là 1/3:
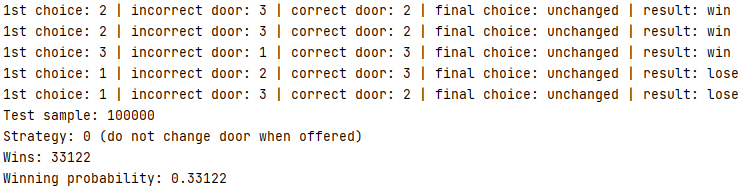
Còn nếu người người chơi chọn lại cánh cửa khác thì tỷ lệ thắng là 2/3:
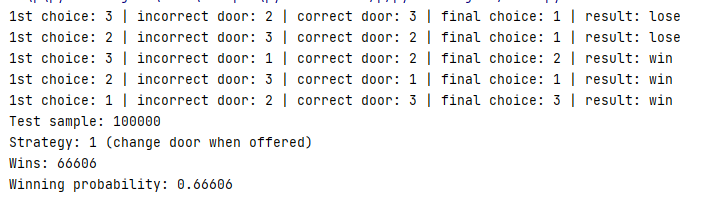
Như vậy là chúng ta đã hoàn thành việc “test thử” Monty Hall có đúng không. Các bạn hãy thoải mái chỉnh sửa code theo ý mình nhé và xem kết quả sẽ thay đổi như nào nhé. Một gợi ý nhỏ: chương trình ở trên, MC luôn chọn cửa sai và khác với lựa chọn của người chơi; nếu người chơi chọn cửa sai và MC mở cửa đó thì tỷ lệ thắng khi người chơi chọn lại cửa là bao nhiêu? Mọi người hãy thử chỉnh sửa code và tìm ra kết quả nhé.
Qua bài viết này, UCC mong mọi người có thể tìm được những mục đích sáng tạo để sử dụng Python: có thể là “test thử” một câu đố nào đó, …. Mong mọi người có thể thấy Python không chỉ dùng để viết những thuật toán nhàm chán :( mà còn là công cụ hữu ích trong mọi việc.
Dưới đây là code đầy đủ:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
# Import thư viện random.
import random
# Chọn một cửa ngẫu nhiên số từ 1 -> 3.
def choose():
return random.randint(1, 3)
# Chọn một cửa ngẫu nhiên trong những cửa chưa được chọn.
def get_unchoosen_door(chosen_doors):
doors_selection = [1, 2, 3]
# Loại bỏ những cửa đã chọn.
for choice in chosen_doors:
if choice in doors_selection:
doors_selection.remove(choice)
# Nếu có một cửa chưa được chọn thì chọn cửa đó. Nếu không chọn ngẫu nhiên 1 trong 2 cửa còn lại.
if len(doors_selection) == 1:
return doors_selection[0]
else:
return doors_selection[random.randint(0, 1)]
# List để lưu lại các kết quả
RESULTS = []
# Variable lưu lại số lượt thắng
WINS = 0
# Strategy (chiến thuật) 0: giữ nguyên lựa chọn ban đầu.
# strategy (chiến thuật) 1: đổi cửa.
STRATEGY = 1
# Số lượt thử
TEST_SAMPLE = 100000
for test in range(TEST_SAMPLE):
# Variable lưu lại kết quả của mỗi lượt.
result = ""
# Chọn ngẫu nhiên một cửa đúng.
correct_door = choose()
# Người chơi chọn một cửa.
first_choice = choose()
# MC mở một ra một cửa sai.
# Lưu ý: mc luôn mở ra cửa sai và không phải là cửa người chơi đã chọn.
incorrect_door = get_unchoosen_door([first_choice, correct_door])
# Lưu lại lựa chọn.
result += f"1st choice: {first_choice} | incorrect door: {incorrect_door} | correct door: {correct_door}"
if STRATEGY:
# Nếu chọn chiến thuật 1 người chơi sẽ đổi cửa.
final_choice = get_unchoosen_door([first_choice, incorrect_door])
result += f" | final choice: {final_choice}"
else:
# Nếu chọn chiến thuật 0 người chơi sẽ giữ nguyên lựa chọn ban đầu.
final_choice = first_choice
result += " | final choice: unchanged"
if final_choice == correct_door:
# Nếu người chơi chọn đúng cửa, tăng số lượt thắng lên 1
WINS += 1
result += " | result: win"
else:
result += " | result: lose"
# Thêm kết quả của lượt chơi vào list các kết quả
RESULTS.append(result)
# In ra một số kết quả mẫu
for r in range(5):
print(RESULTS[r])
# In ra tổng kết.
print(f"Test sample: {TEST_SAMPLE}")
print(f"Strategy: {STRATEGY} ({'change door when offered' if STRATEGY else 'do not change door when offered'})")
print(f"Wins: {WINS}")
print(f"Winning probability: {WINS / TEST_SAMPLE}")